- r
- SQL
- 오라클
- 기초다지기
- 빅데이터분석기사
- 정보처리기사
- 네이버부스트캠프
- 인공지능기초다지기
- Machine Learning
- Ai
- DB
- 데이터 분석 기반 에너지 운영 관리자 양성 및 취업과정
- boostcourse
- 빅분기
- 파이썬
- 코딩테스트 python
- python
- 빅데이터 분석 기반 에너지 운영 관리자 양성 및 취업과정
- 데이터베이스
- PY4E
- 이기적
- [멀티잇]데이터 시각화&분석 취업캠프(Python)
- AI 플랫폼을 활용한 데이터 분석
- 난생처음 R코딩&데이터 분석 저서
- Oracle
- boostcoures
- 코딩테스트
- 이것이 취업을 위한 코딩테스트다 with 파이썬
- 부스트코스
- 프로그래머스
- Today
- Total
매일공부
[AI 기초 다지기] 행렬matrix이란? 본문
1) 행렬matrix 이란?
- "행(row)벡터"를 원소로 가지는 2차원 배열
>> 배열(array)이란? 동일한 데이터 타입의 하나 이상의 값을 저장하는 구조, 1차원 구조
>> 2차원 배열 : 1차원 배열들의 집합, 1차원 벡터들의 집합
- 행(row)와 열(column)이라는 인덱스index를 가짐
- 표기 순서 : 행row - 열col
- 행렬의 특정 행(열)을 고정하면 행(열)벡터라 부름

- 파이썬 스타일 코드로 표현한 벡터
- 각 데이터의 이름을 함께 표현 >> 딕셔너리로 표현
- 데이터의 위치나 순서가 바뀌지 않아야 한다면 >> 튜플로 저장
vector_a = [1, 2, 10] #리스트로 표현
vector_b = (1, 2, 10) #튜플로 표현
vector_c = {'x':1, 'y':2, 'z':10} #딕셔너리로 표현
- 전치행렬transpose matrix
: 행n과 열m의 인덱스가 바뀐 행렬
: X의 상단에 T표시

matrix_a = [[1,2,3], [4,5,6]]
result = [[element for element in t] for t in zip(*matrix_a)]
print(result) #[[1, 4], [2, 5], [3, 6]]*로 행렬 언패킹
>> zip()으로 같은 인덱스끼리 묶음 == [1,4], [2,5], [3,6]
>> 그대로 리스트에 들어감 == 전치행렬
2) 행렬 이해하기
- 벡터 = 공간에서의 한 점
- 행렬 = 여러 점들
- 행렬의 행벡터 Xi는 i번째 데이터
- 행렬의 Xij = i번째 데이터의 j번째 변수의 값 > 행렬은 데이터의 모임

- 행렬은 벡터공간에서 사용되는 연산자operate로 이해
- m차원과 n차원을 연결시켜주는 것으로 생각해볼 수 있음
> 즉, 행렬곱을 통해 벡터X를 다른 차원의 공간 벡터Z으로 보내주는 연산자
> 행렬A와 벡터X를 곱해서 새로운 벡터Z 생성
- 행렬곱을 통해 패턴 추출 및 데이터 압축 가능
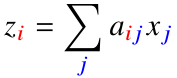

# [1행] [2행]
matrix_a = [[3,6], [4,5]]
matrix_b = [[1,1], [1,1]]
matrix_c = {(0,0):3, (0,1):6, (1,0):4, (1,1):5}
#(0,0):3, (0,1):6
#(1,0):4, (1,1):5
3) 행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱
- 행렬끼리 같은 모양(크기)을 가지면 덧셈, 뺄셈 가능
(벡터의 덧뺄셈과 유사 - 각 인덱스 값이 같은 위치에 있는 값끼리 연산)
- 성분곱은 벡터와 동일 > 각 인덱스 위치끼리 곱함
- 스칼라곱도 벡터와 차이 없음 > 모든 성분에 똑같이 숫자 곱함 : 분배 법칙


u = [2, 2]
v = [2, 3]
z = [3, 5]
result = [sum(t) for t in zip(u, v, z)]
print(result) ##zip() > [2,2,3], [2,3,5] 반환 >> [2+2+3], [2+3+5]
#[7, 10]
matrix_a = [[3,6], [4,5]]
matrix_b = [[5,8], [6,7]]
result = [[sum(row) for row in zip(*t)] for t in zip(matrix_a, matrix_b)]
#zip() : ([3, 6], [5, 8]), ([4, 5], [6, 7])
# > zip(*t) : ((3,5), (6,8)), ((4, 6), (5, 7))
# >> sum : [3+5, 6+8], [4+6, 5+7]
print(result)
#[[8, 14], [10, 12]]
## 스칼라곱-벡터 ##
u = [1, 2, 3]
v = [4, 4, 4]
alpha = 2
result = [alpha * sum(t) for t in zip(u,v)]
print(result) #[7, 10]
4) 행렬의 동치
- 2개의 행렬이 서로 같은지를 나타냄
- A = B : 2개의 행렬이 동치
- all() 함수 : and 조건, 모든 값이 참일 경우에만 True
- any() 함수 : or 조건, 하나라도 참이 있으면 True, 모두가 거짓일 때만 False
matrix_a = [[3,6], [4,5]]
matrix_b = [[1,1], [1,1]]
all([row[0] == value for t in zip(matrix_a, matrix_b) for row in zip(*t) for value in row])
#False
## 코드 이해하기 ##
matrix_a = [[3,6], [4,5]]
matrix_b = [[1,1], [1,1]]
for t in zip(matrix_a, matrix_b):
print("t:", t, type(t)) #t: ([3, 6], [1, 1]) <class 'tuple'>
for row in zip(*t):
print("row:", row, type(row)) #row: (3, 1) <class 'tuple'>
for value in row:
print("value: ", value) #value: 3 value: 1
print(row[0] == value) #True False #False가 최종
# >> 이렇게 반복되면서 전체 같아야 True 반환
5) 행렬 곱셈 matrix multiplication
- i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬 계산
- 행렬곱은 X의 열의 개수와 Y의 행의 개수가 같아야함
- XY != YX : X와 Y의 순서 달라지면, 계산하는 값들도 달라짐 > 즉, 순서 매우 중요
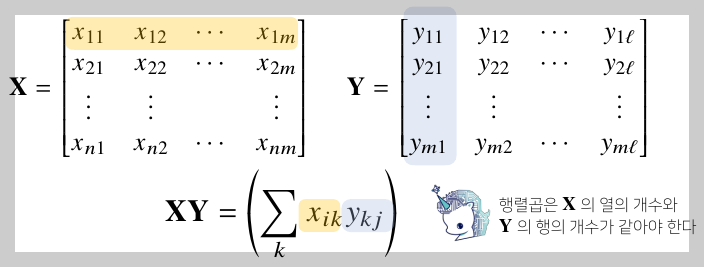
matrix_a = [[1,1,2], [2,1,1]]
matrix_b = [[1,1], [2,1], [1,3]]
result = [[sum(a*b for a,b in zip(row_a, column_b)) for column_b in zip(*matrix_b)] for row_a in matrix_a]
print(result) #[[5, 8], [5, 6]]
6) 역행렬inverse matrix 이해하기
- 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬
- 곱하는 순서와 상관없이 항등행렬로 돌아옴
> 항등행렬 : 임의의 벡터(또는 행렬)을 곱해줬을 때, 자기 자신이 나오게 되는 행렬
- 행과 열 숫자가 같고[n = m] & 행렬식determinant이 0이 아닌 경우에만 계산 가능

- 역행렬 계산 불가일 때 : 유사역행렬pseudo-inverse OR 무어펜로즈Moore-Penrose 역행렬 A+ 이용
n = 열 // m = 행

> 파이썬의 numpy 계산 & 행렬의 내적 & 응용은 추후에 numpy를 배운 뒤에 링크 or 내용 추가 예정
'IT > 기초 다지기' 카테고리의 다른 글
| 데이터 과학 [기본지식] (0) | 2022.11.19 |
|---|---|
| [AI 기초 다지기] 벡터란? (0) | 2022.07.23 |
| [AI 기초 다지기] jupyter notebook 단축키 정리 (0) | 2022.07.23 |
| [AI 기초 다지기] Windows & cmd 명령어 정리 (0) | 2022.07.23 |
| [CS50 2019] 컴퓨팅 사고 Computational Thinking (0) | 2022.07.22 |
