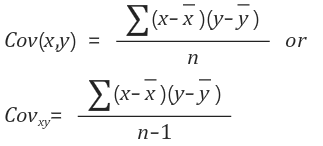- 빅분기
- r
- 인공지능기초다지기
- Ai
- SQL
- Machine Learning
- 데이터베이스
- 코딩테스트 python
- Oracle
- 기초다지기
- 이것이 취업을 위한 코딩테스트다 with 파이썬
- 오라클
- PY4E
- python
- boostcourse
- 빅데이터분석기사
- boostcoures
- 이기적
- 정보처리기사
- 난생처음 R코딩&데이터 분석 저서
- DB
- 네이버부스트캠프
- 프로그래머스
- 부스트코스
- 코딩테스트
- AI 플랫폼을 활용한 데이터 분석
- 데이터 분석 기반 에너지 운영 관리자 양성 및 취업과정
- 빅데이터 분석 기반 에너지 운영 관리자 양성 및 취업과정
- 파이썬
- [멀티잇]데이터 시각화&분석 취업캠프(Python)
- Today
- Total
매일공부
[Machine Learning] 회귀의 가설검정&분산분석 본문
회귀의 프레임워크
| 반응변수(target) | 설명변수(feature) | 대표 방법론 | |
| 있음 | 회귀 | 범주형 | - T-검정 - 분산 분석 |
| 수치형 | - 상관 분석 | ||
| 수치형/범주형 | - 선형 회귀 | ||
| 분류 | 범주형 | - 카이제곱 검정 - 피셔의 정합 검정 - 코크란-맨틀-핸첼 검정 - 맥니마 검정 |
|
| 수치형/범주형 | - 로지스틱 회귀 - 포아송 회귀 - 서포트 벡터 머신 - 선형 판별 분석 |
||
| 수치형/범주형 | 수치형/범주형 | - K최근접 이웃 -트리 기반 모형 |
|
| 없음 | 수치형 | - 주성분 분석 - 군집 분석 |
|
| 범주형 | - 연관성 분석 | ||
가설 설정
- 귀무가설(Null Hypothesis) H0 – 영 가설, 모집단에 대한 기존의 생각 (부정적, 소극적, 보수적, 전통적)
- 대립가설(Alternative Hypothesis) H₁ - 귀무가설과 다른 새로운 생각 (주장하고 싶은 것; 긍정, 적극, 진취, 미래지향)
- 가설검정
: 표본의 데이터를 근거로 귀무가설과 대립가설 중에서 하나를 선택하는 과정
: 모집단에 대합 주장에 대해 표본을 추출하여 수집된 데이터에 근거하여 주장이 맞다고 할수 있는지를 통계적으로 검정하는 것
가설설정예시>
A 온라인 쇼핑몰'에서 상품 페이지 내 Buy 버튼의 위치를 두고 A/B Test를 진행한다
귀무가설 : A와 B는 유의미한 차이가 없다
대립가설 : A와 B는 유의미한 차이가 있다
코로나 바이러스 치료를 위해 개발된 A약이 실제로 효과가 있는지 보고 싶다
귀무가설 : A약은 효과가 없다
대립가설 : A약은 효과가 있다
유의수준과 유의확률(p-value)
- 유의확률 p-value : 귀무가설이 옳다는 가정 하에 검정 통계량이 계산될 확률
- 유의수준
: 귀무가설 또는 대립가설의 기준점
: 귀무가설이 옳은데 실수로 기각될 확률(1종 오류)를 범하게 될 확률을 최소화하기 위한 1종 오류의 상한선
- 유의수준 > p-value : 대립 가설을 채택
유의수준 < p-value : 귀무 가설을 유지

- p-value값의 유의수준은 일반적인 문제에서는 0.05,
> 암진단과 같은 문제 에서 p-value값의 유의수준은 0.01로 하기도 함
- 1종 오류 : 귀무가설이 사실인데 기각했을 경우(기존의 것에서 새로운 것으로 갈아타야하기에 비용이 많이 들어서 더 큰 문제)
- 2종오류 : 귀무가설이 거짓인데 채택했을 경우(기존의 것을 다시 수정하는 정도, 비용이 1종오류보단 적게 소모)
검정 통계량 계산(포본추출)
검정 통계량 = ( 표본 평균 - 모평균 ) / 표본표준편차
- 표본 데이터에서 계산되어 가설 검정에 사용하는 랜덤 변수
- 검정 통계량을 사용하여 귀무 가설의 기각 여부 확인
| 가설 검정 | 검정 통계량 |
| z-검정(모집단의 분산 known) | z-통계량 |
| t-검정(모집단의 분산 unknown) | t-통계량 |
| 분산 분석 | F-통계량 |
| 카이제곱 검정 | 카이제곱 통계량 |
- t-검정의 검증 방법
(1) 표본에 대해 t-검정 통계량 값을 계산합니다(-4에서 4 정도 사이의 값을 얻습니다).
(2) 값이 t-분포 그래프의 양 끝에 속할수록 모집단과 평균이 다르다는 것을 보여 줍니다.
(3) 지정한 유의확률(%)을 사용하여 유의 값을 선정하고 검정합니다.
- 참고: https://thebook.io/080246/part04/ch15/unit32-12/
가설검정종류
가설검정 (검정대상)
1. 평균
2. 분산
1. 가설검정(평균) 모집단의 개수
-------단일표본 T검정(1개-정규성 가정)
-------대응표본 T검정 (동일표본 2개, 정규성 만족)
------ 윌콕스 검정 (동일표본 2개, 정규성 만족X)
------ 독립이표본T검정 (다른표본 2개, 정규성, 독립성, 등분산성 만족)
-------분산분석 ANOVA(모집단 3개이상)
------(독립변수 1, 종속변수 1 ) 일원분산분석
------(독립변수 2, 종속변수 1 ) 이원분산분석
------(독립변수>= 1, 종속변수 1 ) 다원분산분석
------(독립변수>= 1, 종속변수>= 1 ) 다변량분산분석
2. 가설검정(분산) 모집단의 개수
------- 카이제곱검정(1개)
------- F검정 (2개)
t-검정(t-test)
- 단일표본 t검정(One sample t-test)
- 한 개의 모집단을 이루고 있는 양적 자료의 모평균이 이전보다 커졌는지, 작아졌는지 변화가 있는지를 통계적으로 검정하는 방법
- 모수 검정법인 t 검정은 표본 수가 작은 경우에 평균을 비교하는 방법
- 단일표본 t 검정의 기본 가정? 정규성
- 기본 가정사항을 만족하지 못하면 비모수 검정으로 분석
- 양적자료 < 5000 이면 샤피로-윌크 테스트
양적자료 >= 5000 이면 앤더슨-달링 테스트 - A 유통은 이번 달에 새로운 프로모션을 기획했다
귀무가설 : 프로모션은 매출증가에 영향을 주지 않는다 (프로모션 진행 매출증 = 프로모션 진행하지 않은 매출 )
대립가설 : 프로모션은 매출증가에 영향을 준다 (프로모션 진행 매출증 ≠ 프로모션 진행하지 않은 매출 )
A대학 남학생의 평균 키가 175인지 아닌지를 보고자 한다
귀무가설 : 평균 키는 175와 같다 ( 차이가 없다)
대립가설 : 평균 키는 175와 같지 않다 ( 차이가 있다)
>> 정규성 검정(normality test)
- 목적
1. 단순히 정규 모집단이 맞는지 확인하기 위해서
2. 정규 모집단이라는 것이 확인되면 모수 검정을 하고, 아니면 비모수 검정을 하기 위해서 - p-value < 0.05 = 정규 모집단이 아니라는 결론 >> 비모수 검정 선택
- p-value > 0.05 = 모수 검정 선택
- 표본 수가 커지면 검정력(power)이 높아진다(p-value가 작아진다)
- 표본 수가 충분히 크다면 정규 모집단이라는 가정도 필요 없이 z 검정으로 평균을 비교해도 된다
- 정규성 검정의 목적이라면, 표본 수가 충분히 큰 경우에는 정규성 검정을 할 필요도 없이 바로 모수 검정을 선택하면 된다
>> 중심극한정리(central limit theory)
- 모집단에서 표본이 충분히 크다면(약 30개 이상), 이 표본평균의 분포는 정규분포에 근사하다
- 유의수준 p값 > 0.05 클수록 좋은 것 3가지
첫째, 정규성 검정
둘째, 등분산성
셋째, 적합도
>> 등분산검정(Equal-variance test)
- 두 정규성을 만족하는 두 개의 데이터 집합으로부터 두 정규분포의 모분산이 같은지 확인 하기 위한 검정
- 단측 검정, 양측검정으로 수행할 수 있음
- 전제 조건 = 정규성이 존재해야 한다
> 귀무가설 : 등분산성이 있다(분산의 차이가 없다)
> 대립가설 : 등분산성이 없다 (분산의 차이가 있다) - scipy의 stats에서 이를 위한 bartlett, fligner, levene 명령을 제공
> 바틀렛 Bartlett : 정규성에서 벗어나는 것에 민감 => 단순히 비정규성을 결정하는 것과 유사
> 레빈 Levene : bartlet의 대안, 바틀렛보다 덜 민감. 정규분포에서 더 나은 성능을 보임
> 플리그너 Fligner: 비모수
> https://freedata.tistory.com/24
- 독립 2표본 검정(Two sample test)
- 두 개의 독립적인 모집단에 대한 평균에서 통계적으로 유의미한 차이가 있는지를 검정하는 방법
- 독립 2표본 검정(Two sample test) 기본 가정? 정규성 득립성 등분산성
- 평균은 모집단을 대표하는 값이다.
- 귀무가설 : A집단의 평균과 B집단의 평균은 같다
대립가설 : A집단의 평균과 B집단의 평균은 같지 않다 - 유의 수준 = 0.05
- 귀무가설과 대립가설 중 하나를 선택하기 위해서 모집단에서 표본을 추출하여 평균을 구함
- A 표본의 평균 - B 표본의 평균 = 0 이면 귀무가설에 가까울 것이고
A 표본의 평균 - B 표본의 평균 ≠ 0 이면 대립가설에 가까울 것이다 - 두 표본의 평균의 차가 0에 가까워도 분포를 알아야 0에서 가까운지 알 수 있다
- 남학생과 여학생의 성적 샘플을 비교한다.
귀무가설 : 두 집단의 성적 평균은 같다(차이가 없다)
대립가설 : 두 집단의 성적 평균은 같지 않다(차이가 있다)
- 대응표본 t검정
- 실험 전후에 데이터를 수집한 두 데이터 간 평균 차이를 검증하는 것
- 전제 조건 = 데이터에 정규성이 존재해야 한다
- 분석과정 :
정규성 검정(샤피로 윌키 테스트)
scipy.stats.shapiro(data)
=> 정규성을 만족하지 않으면 (윌 콕슨 검정) scipy.stats.wilcoxon(data1, data2)
정규성을 만족하면 (대응 표본 t검정) scipy.stats.ttest_rel(data1, data2) - Pre에서 Post를 뺀 값으로 정규성 검정
- S전자는 이번에 새로운 광고 모델로 아이돌 스타 A양을 기용했지만 모델료가 비싸서 재계약을 고민한다
귀무가설 : 아이돌스타 광고 전과 후의 매출의 차이가 없다
대립가설 : 아이돌스타 광고 전과 후의 매출의 차이가 있다
50명의 부모들이 "부모가 달라졌어요" 시청했을때 시청 전후 양육방식의 변화가 있는가?
귀무가설 : "부모가 달라졌어요" 시청 후 양육방식의 차이가 없다
대립가설 : "부모가 달라졌어요" 시청 후 양육방식의 차이가 있다
10명의 사격자가 1차 2차 사격을 했을 떄 차수의 평균 변화가 있는가?
귀무가설 : 1차 2차 사격의 평균이 같다.
대립가설 : 1차 2차 사격의 평균이 다르다.
분산 분석

그림 A : ANOVA 분석 결과, 그룹 사이의 차이가 없음
그림 B : ANOVA 분석 결과, 그룹 사이의 유의한 차이가 존재
3개 이상 다수의 집단을 비교할 때 사용하는 가설검정 방법? ANOVA(Analysis Of Variance)
>> 실험계획법(experiment design)이라는 영역에서 주로 사용됨
>> 집단간분산(variance between groups) / 집단내분산(variance within group) 기반의 F분포를 이용
오차의 가정
1. 각 집단 간의 자료는 독립
2. 각 집단의 자료는 정규분포를 따름
3. 각 집단의 모분산은 동일
다수의 집단의 연속형 반응변수 1개, 범주형 설명변수 1개 분산분석 ? 일원분산분석 (One-way ANOVA)
다수의 집단의 연속형 반응변수 1개, 범주형 설명변수 2개 분산분석 ? 이원분산분석 (Two-way ANOVA)
다수의 집단의 연속형 반응변수 1개, 범주형 설명변수 3개 분산분석 ? 다원분산분석
다수의 집단의 연속형 반응변수 2개이상, 범주형 설명변수 1개이상 분산분석 ? 다변량분산분석 (MANOVA : multiple analysis of variance)
다수의 집단의 연속형 반응변수 1개, 범주형과 연속형 설명변수 2개 분산분석 ? 공분산분석 (ANCOVA : analysis of covariance)
두 분산의 비율 통계량 ? F통계량
>> (그룹간의 차이 정도 / 불확실도) 표본 평균 간 퍼진 정도 / 표본 내에서 퍼진 정도
>> F = 집단간 분산 / 집단 내 분산
>> 집단간 분산(분자)이 클수록, 집단 내 분산(분모)이 작을수록 F통계량이 커지며, F통계량이 커질수록 집단간 평균 차가 존재
#일원분산분석
import pandas as pd
from statsmodels.formula.api import ols
df_model = pd.DataFrame(df_oneway, columns=['defRate', 'type'])
results = ols('defRate ~ C(type)', data=df_model).fit()
results.summary()
R-squared: 결정계수, 모델의 설명력(0~1 사이 값), 1에 가까울수록 모델의 설명력이 높음
Prob (F-statistic): p-value
상관 분석

- 수치형인 두 변수 간의 관계를 분석 하는 방법론
- 두 연속형 변수의 선형 상관관계를 분석
- 독립변수, 종속변수 구별X
- 범위 : -1 < p < 1

1에 가까우면 : 양의 상관관계
0이면 : 선형의 상관관계가 아님
-1에 가까우면 : 음의 상관관계
- 공분산
: 확률변수들의 벡터 공간상에서의 내적
: A변수가 변할 때 B변수가 변하는 정도
상관계수 유형
1. 피어슨(Pearson) 상관계수
: 상관분석에서 기본적으로 사용되는 계수
: 이변량 정규분포를 따른다는 분포 가정 필요
: 연속형 변수의 상관관계 측정(신장, 몸무게)
: 모수 검정
2. 스피어만(Spearman) 상관계수
: 비모수 검정
: 변수값 대신 순위로 바꿔서 이용하는 상관계수(학교등급, 졸업학위 level)
: 데이터 내 편자와 에러에 민감하며, 일반적으로 켄달 상관계수보다 높은 값을 가짐
3. 켄달(Kendall) 상관계수
: 비모수 검정
: 변수값 대신 순위로 바꿔서 이용하는 상관계수(학교등급, 졸업학위 level)
: 샘플 사이즈가 적거나, 데이터의 동률이 많을 때 유용
실습코드
from scipy.stats import pearsonr
a = [5.0, 0.5, 4.0, 3.5, 3.5]
b = [5.0, 3.0, 5.0, 5.0, 5.0]
def pearson_similarity(a,b):
return np.dot( (a-np.mean(a)), (b-np.mean(b)) ) / ( (np.linalg.norm(a-np.mean(a))) * (np.linalg.norm(b-np.mean(b))) )
print(pearson_similarity(a,b)) #0.9312661473328351
print(pearsonr(a,b)) #PearsonRResult(statistic=0.931266147332835, pvalue=0.02140725059687241)
print(np.corrcoef(a,b))
# [[1. 0.93126615]
# [0.93126615 1. ]]
ab = [(x,y) for x,y in zip(a,b)]
ab = pd.DataFrame(ab, columns=['a', 'b'])
ab
ab = pd.DataFrame(zip(a, b)) # array를 묶을 때는 zip으로 묶어서 만들어야함
print(ab)
ab.corr(method='pearson')
* 내용참고&출처 : 태그에서 수강한 수업을 복습 목적으로 정리한 내용입니다.
'IT > ML' 카테고리의 다른 글
| [Machine Learning] 조건에 따른 사용가능한 회귀분석 모델 (0) | 2022.12.09 |
|---|---|
| [Machine Learning] 자료의 종류의 따른 회귀분석 모델 (0) | 2022.11.30 |
| [Machine Learning] 교차검증 (0) | 2022.11.21 |
| [sklearn] 학습과 검증셋 분리 (0) | 2022.11.21 |
| [sklearn] Data Preprocessing (0) | 2022.11.21 |